Assignments » PA5: Sampling lights

Triangles

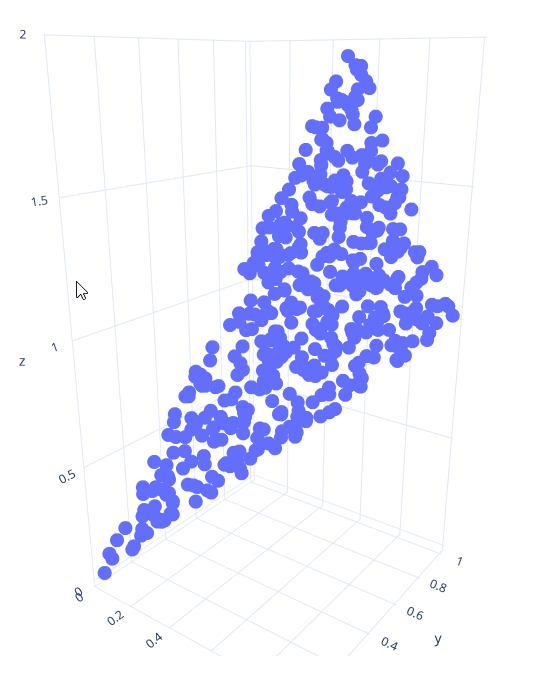
Implement a function sample_triangle() that produces points uniformly at random on a triangle with the specified coordinates. There are different ways you can do this; the easiest way is to first generate random barycentric coordinates (alpha, beta, gamma), and then return the corresponding interpolated point v0*alpha + v1*beta + v2*gamma.

Also implement the corresponding sample_triangle_pdf() function.

Visualize points from your function for a triangle with corners (0,0,0), (1,1,1) and (0.5, 1, 2). You should get points like the ones shown in the image here.

Spherical Cap

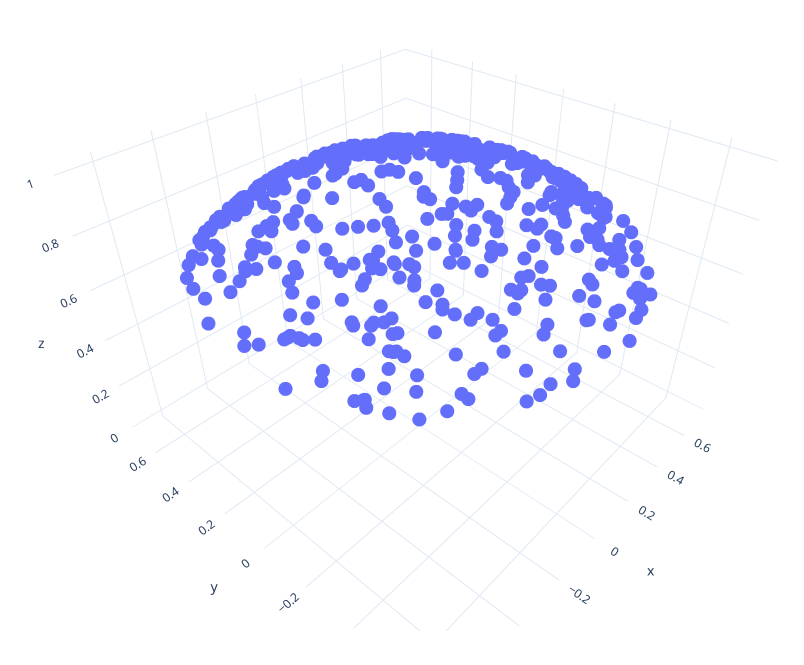
Now implement the function sample_sphere_cap() to sample points uniformly at random from a spherical cap. You've already (implicitly) implemented this method for your previous assignment: Sampling the sphere and the hemisphere are just special cases of sampling different sections of the sphere. Copy-paste the code for sampling the hemisphere from your previous assignment; all that needs to change is the computation of cos_theta: It should be distributed uniformly between 1 and cos_theta_max; this is the cosine of the largest angle that points are allowed to have with the normal. In pseudo code, cos_theta = lerp(cos_theta_max, 1.0f, <uniform random number>).

Also implement the corresponding sample_sphere_cap_pdf() function.

Visualize your code for an angle of pi/4 (Hint: You pass the cosine of the angle to this function, not the angle directly). It should look something like the image shown here.

Rectangles

To help you get started with sampling surfaces, we provide working implementations of Quad::sample() and Quad::pdf() in quad.cpp.

Quad::sample(), generates a random point on the rectangle, stores it in rec.hit.p, and computes the normalized direction from rec.o to this point, along with the PDF and other members of the EmitterRecord. It then returns the emitted color of that surface point divided by the PDF.

Quad::pdf(), checks if the given direction hits the Quad from the given origin o. If not, it returns 0; otherwise, it returns 1/area times the geometry factor.

You can test this code using the sample tester tool by running:

darts scenes/assignment5/test_surfaces.json

You should get images like these for quad-pdf.png and quad-sampled.png:

Triangles

Now add and implement Triangle::sample() and Triangle::pdf() (we've already implemented Triangle::is_emissive() for you). Use exactly the same recipe as you did for the quad - all that needs to change is how to get a point on the surface, and the computation of the surface area. Look at Triangle::intersect() for inspiration for how to get the three corners of the triangle (p0, p1 and p2).

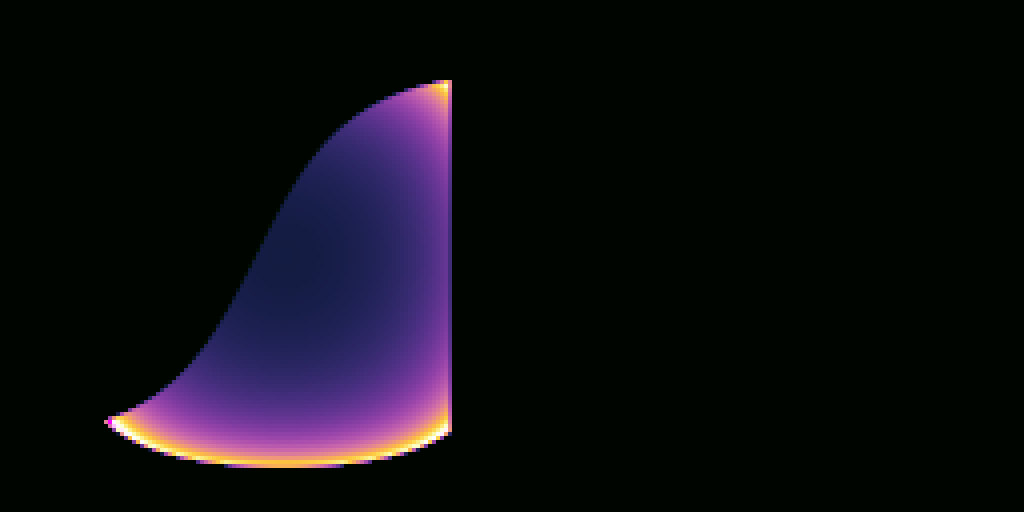
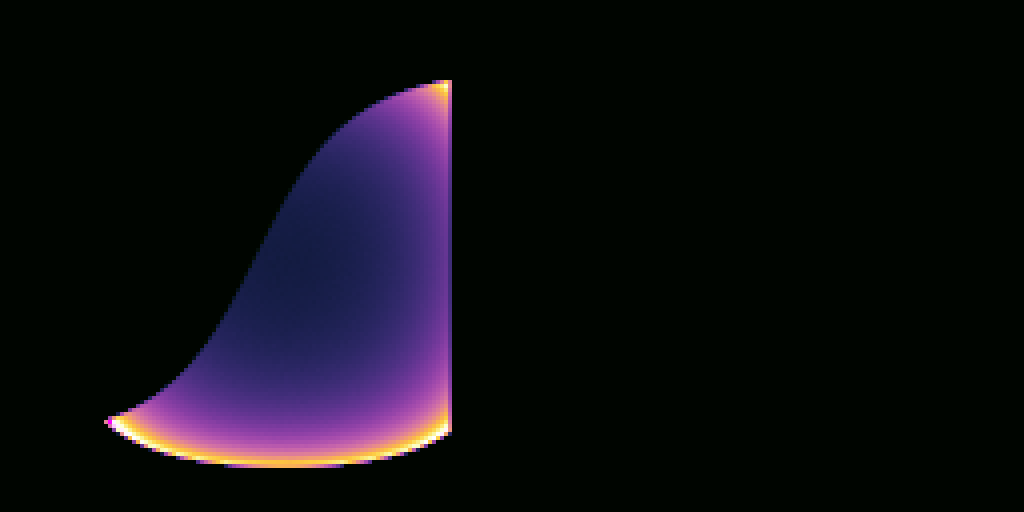
Spheres

Open sphere.h and sphere.cpp, and add and implement Sphere::sample() and Sphere::pdf() (we already provide you XformedSurfaceWithMaterial::is_emissive(), which Sphere inherits).

We will use a different approach for sampling the sphere: Instead of sampling a point on the sphere first and computing the direction towards it, we will directly sample the cone of directions that all point towards the sphere. To do this, you can use your function for sampling spherical caps from the first task. However, to use this function you need to first figure out cos_theta_max, the angular extent of the sphere as seen from rec.o. You can compute it with cos_theta_max = sqrt(d*d - r*r)/d where d is the distance from the center of sphere to rec.o, and r is the radius of the sphere. Hint: Can this formula fail? When does this happen? What should the value of cos_theta_max be in that case? Note that the sphere may be transformed by a Transform, so r may not simply be Sphere::m_radius. You may assume that the Transform contains only isotropic scaling and rotation. How can you compute the resulting radius in that case?

The sampling function you implemented in Task 1 assumes the spherical cap is aligned with the z axis. You should use your ONB class to transform the sampled direction, so that the spherical cap points from rec.o towards the center of the sphere instead.

For Sphere::pdf(), you should first check if the ray with the given origin/direction intersects with the sphere. If it does, the PDF is simply 1/solid angle of the spherical cap (no geometry factor needed - we generated directions directly!). The solid angle of a spherical cap with opening angle of theta_max is 2*pi*(1-cos(theta_max)).

Test your code with the sample tester tool by running the scene scenes/assignment5/test_surfaces.json again. You should get images like these:

Surface Groups

Open surface_group.h and surface_group.cpp and implement the sampling interface for the SurfaceGroup class. This class represents a collection of shapes (e.g. the list of all lights in the scene), which are stored in the array m_surfaces.

In your implementation of SurfaceGroup::sample(), we should first pick one of the children uniformly at random, and then call that child surface's sample() function. We already give you functions that provide some of this functionality. Read the documentation for the functions Surface::sample_child() and Surface::child_prob() in surface.h. For a single surface, these functions default to return the surface itself. We also provide a specialization of this function for SurfaceGroup. Look at its implementation in surface_group.cpp. This function selects one of the child surfaces at random, and returns a pointer to it, along with the probability it was chosen. You can call this function in your implementation of SurfaceGroup::sample(). Since you are only returning the color of one of the children with some probability, you will need to adjust the color returned by the child's Surface::sample() function. Also, before returning, make sure that the EmitterRecord::pdf data member accounts for both the probability of selecting a particular light (returned by SurfaceGroup::sample_child()), and the probability density within that light (returned by Surface::sample()).

For pdf(), the Shirley book suggests calling the pdf() method of each surface in the list and returning the average of all the PDF evaluations. We already provide you an implementation of SurfaceGroup::pdf() in surface_group.cpp. However, while this will work, it requires us to iterate over all emitters in the scene, which takes time. This will work fine for a few emitters, but once you turn an entire Mesh into an emitter, it will be a significant bottleneck.

To make this faster (and O(1) complexity!) we will not use SurfaceGroup::pdf() at all. When needed, we will instead compute the effective PDF as the product of the child selection probability (SurfaceGroup::child_prob()) and the pdf returned by the selected child's Surface::pdf() function.

Test your code with the sample tester tool by running the scene scenes/assignment5/test_surfaces.json again. You should get images like these:

Direct Lighting Material Integrator

First make sure your PathTracerMats integrator from the last assignment can successfully render scenes/assignment4/veach_mats.json to produce a direct illumination image like the one shown here when ‘"max bounces"’ is set to 1.

Most of this image looks extremely noisy, especially the background and the reflections in the lower right. We can do better than this!

Creating a list of scene emitters

Instead of asking the Material to generate ray directions for us, we could instead generate ray directions by sampling points on all surfaces in the scene using our new Surface::sample() function. As it is now, however, this would not be so useful, since most surfaces in the scene do not emit light. We'd like to sample rays towards surfaces that emit light. To do that we first need to add some plumbing to our code to allow a Scene to maintain a list of only the emissive surfaces.

First, add a SurfaceGroup m_emitters; data member to the Scene class. Then, take a look at Scene::add_child(). Currently it just calls m_surfaces->add_child(). After doing so, check whether the surface is emissive (call the is_emissive() method on surface) and if it is, also add surface to m_emitters by calling its add_child method.

Next Event Integrator

Add a new integrator class called PathTracerNEE, and register it with the factory using the string "path tracer nee". The "NEE" part stands for Next Event Estimation, which is a fancy name for sampling light sources directly. We will start by implementing direct lighting with no recursion first.

On a basic level, this integrator looks very similar to the material-based integrator from the previous subtask (and you can start by copy-pasting that code and removing the recursion). However, instead of calling Material::sample() to produce a direction, it should call scene.emitters().sample(). scene.emitters() is a SurfaceGroup that contains all emissive shapes in the scene. Similarly, instead of dividing by Material::pdf(), you should divide by the EmitterRecord::pdf field populated by scene.emitters().sample().

This (for the first time) shows the flexibility of the Monte Carlo approach: All you had to change was the sampling and PDF routine, and you get a noise-free image much faster! This would not have been possible with the renderer you wrote in Assignment 1. Convince yourself that this integrator has much less noise by running your new code on scenes/assignment5/veach_nee.json. You should get an image looking like the one shown here.

This looks much better than the PathTracerMats integrator for most of the image... except for the upper left, where the NEE estimator does much worse. Just like discussed in class, we'll fix this by combining both estimators with MIS in the next section. Also beware that this new estimator will not (yet) work correctly if you set "max bounces" > 1. We'll handle that further in this assignment.

Additional verification

But before we do, we've designed a few more scenes to help you debug and verify your implementation.

If the Veach scene isn't rendering correctly, it can be difficult to isolate the issue because it tests multiple features simultaneously. We provide a simpler set of scenes to help you debug your sphere lights and integrators. They are scenes/assignment5/sphere_light_[small|medium|large]_XXX.json. These scenes rely on the principle that two fully visible sphere lights will produce identical illumination on a diffuse surface even if their radii are different, as long as their power is the same.

The Veach scene uses sphere lights, but let's also test triangle lights. Render the scenes/assignment5/odyssey_triangle_mats.json and scenes/assignment5/odyssey_triangle_nee.json and scenes. This scene is identical to the one from the previous assignment, but the rectangular light source is composed of two Triangles instead of a single Quad. Compare these triangle versions to the quad versions in scenes/assignment4/odyssey_mats.json and scenes/assignment5/odyssey_nee.json.

MIS Integrator

Add a new integrator class called PathTracerMIS, and register it with the factory using the string "path tracer mis". The MIS part stands for Multiple Importance Sampling, which is a technique for efficiently combining multiple integration techniques.

Begin by copy-pasting either your PathTracerMats or your PathTracerNEE integrator from before. Instead of always sampling from the material, or always from the light source, you should sample from a mixture of both of them. With probability of 0.5, generate a direction by sampling the material; otherwise, generate a direction by sampling the lights. After you've generated a direction, trace a ray and evaluate the emission and material like before; however, instead of dividing by just the material pdf or the light PDF, divide by the average of the two PDFs (since you randomly sample from either one).

To compute the average PDF you will need to evaluate both PDFs for either sample you generate. Material::pdf() allows you to evaluate the material sampling PDF for any direction. For a sample generated with SurfaceGroup::sample(), we also get its PDF in the EmitterRecord::pdf field. The potential remaining tricky part is evaluating the emitter PDF for the ray sampled by the material. If you are an undergraduate, you can use our provided SurfaceGroup::pdf() function. Graduate students (and undergraduates for extra credit) should avoid this function. Instead, you can compute this by noting that our SurfaceGroup::sample() procedure works in two steps: first sample a child surface, and then sample a point on the child surface. The probability of the first we can obtain by calling scene.emitters()->child_prob(). Once we hit a surface with our material-sampled ray, we can call its Surface::pdf() function to account for the probability density of the second step.

Test your integrator on scenes/assignment5/veach_mis.json and compare to the NEE and material sampling variants. You should get images like those below:

The integrator now works robustly in all parts of the scene, and combines the good traits of both material sampling and light sampling.

Also test your integrators on scenes/assignment5/odyssey_triangle_XXX.json. Here is our comparison:

Full Path Tracing

Now extend the PathTracerMIS integrator from the previous subtask to do not just direct lighting, but all direct and indirect lighting. Your code currently finds the closest hit point along the given ray, estimates direct lighting at that location and exits. All you need to do in order to support indirect light is to add recursion before exiting: After computing direct lighting, sample the material to obtain the next ray along the path, and call the function recursively (or in a loop) with the new ray to obtain an estimate of indirect lighting. Divide that estimate by the material sampling PDF, and add this estimate to the direct lighting estimate. That's it!

Optional: You could complete your PathTracerNEE integrator to compute full global illumination in exactly the same way. Just generate a recursive ray by sampling the material in addition to the (non-recursive) shadow ray towards the lights.

Grad Students: Optimize your PathTracerMIS integrator. In the current version, you sample the material and trace a ray once for direct lighting, and a second time for the recursive ray. This is wasteful - they can both use the same ray and intersection (intersecting the scene is expensive!). Optimize your implementation to reuse the material ray and intersection for the recursive call. You can check the lecture slides for ideas on how to do this.

Test your new integrators on scenes/assignment5/jensen_box_XXX.json.